La scuola in cui ci si
ammala.
I
mali, le delusioni e le contraddizioni dell'insegnamento e del sistema scolastico
italiano, analizzati da uno studente liceale. Di Lorenzo Picinali, tesina di
maturità scientifica, a.s. 1999/2000. Novembre 2000.
prima parte
"Quando mai a scuola si impara qualcosa perché se ne ha davvero bisogno o perché si è mossi da una vera curiosità? Ci fu detto quali erano le regole della sintassi, la tassonomia delle piante e i quadri di Raffaello. Ma lo capimmo, lo imparammo davvero in quel momento, in quel trimestre, per superare l'interrogazione? [...]
Non c'è cultura senza piacere mentale, non c'è studio senza passione. Altrimenti, a scuola ci si ammala".
Alfonso Berardinelli
[...]
[...]
"C'era una volta una scuola in cui ci si ammalava.
Li dentro i ragazzi passavano le ore più noiose della loro vita seduti ad ascoltare una persona che cercava di insegnare qualcosa di utile, ma in realtà faceva disimparare al povero ragazzo tutto ciò che di più bello c'era nella vita: il gioco, la libertà e la felicità..."Ho avuto il privilegio e la fortuna di poter concentrare tutta la mia vita di giovane sulla scuola, ma ho scelto di non farlo, e vorrei spiegarne il perché.
Non ho nulla di personale contro i professori, ma sono contro l'istituzione scolastica nel modo in cui è concepita ora; non si "guarisce" la scuola con inutili e blande riforme come quelle varate negli ultimi anni: quello che non funziona è qualcos'altro!
La "storia" che voglio raccontare in queste pagine non ha molto di diverso da questa, se non il tempo:
"C'è una scuola in cui ci si ammala...
1. (FISICA)
Vorrei raccontare un episodio che mi è accaduto qualche mese fa:
mi trovavo a casa di un amico coetaneo che come hobby ripara radio e televisioni, qualche volta mi capita di passare da lui per provare a seguirlo in una delle sue riparazioni, e lo stavo osservando mentre saldava uno strano componente su di un circuito; spinto dalla curiosità gli chiesi di che componente si trattasse, e lui mi rispose: "E' un semplice condensatore di tensione".
A quel punto "sfoderai" mentalmente tutte le mie conoscenze fisiche su quello strumento:Due lastre metalliche aventi cariche opposte e poste l'una di fronte all'altra ad una distanza piccola rispetto alle loro dimensioni, costituiscono un condensatore.
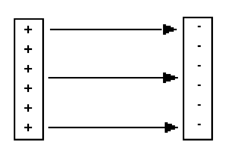
Tra le due piastre, che vengono dette armature, si forma un campo elettrico, le cui linee di forza sono parallele e vanno dall'armatura carica positivamente a quella carica negativamente; l'intensità del campo elettrico prodotto da un condensatore è uguale alla somma dei campi elettrici generati dalle due armature. Possiamo osservare che i campi elettrici prodotti dalle singole piastre all'esterno si sottraggono mentre all'interno si sommano.
Tenendo conto che il campo elettrico di ciascuna armatura è costante ed è espresso dalla relazione:
E=o/2eo dove: o=omega=densità superficiale di carica della lastra;
eo=epsilon 0=costante dielettrica nel vuoto;
concludiamo che il campo elettrico di un condensatore all'esterno è nullo, mentre nello spazio compreso tra le due armature è costante e uguale al doppio del campo prodotto da una piastra, perciò:
E=o/eo Ogni condensatore ha una sua capacità, che è definita dal rapporto:
C=Q/V2-V1 dove V1 e V2 sono rispettivamente i potenziali dell'armatura negativa e di quella positiva, e Q è la carica di ciascuna armatura; poiché i potenziali V dipendono direttamente dalla carica Q, si può notare che la capacità non dipende dalla carica sulle armature, ma dalla geometria del condensatore stesso e dal dielettrico interposto tra le armature.
Tutto ciò che potevo dire sul condensatore era questo, ed effettivamente mi sentivo molto fiero di me per tutto quello che ricordavo. Ma, a pensarci bene, non sapevo assolutamente dire a che cosa servisse un condensatore in un circuito; così, con un po' di vergogna, chiesi al mio amico (che aveva fatto solamente la terza media) una breve spiegazione, e lui mi rispose:
Il condensatore di tensione è uno strumento che serve a mantenere un segnale stabile, cioè a "pulire" l'alimentazione, assorbendo gli eccessi e compensando i difetti; oppure può anche essere utilizzato per dare una grande quantità di energia in poco tempo: messo in serie con una resistenza, accumula tensione tanto quanto la sua capacità gli permette, dopodiché la scarica tutta in un tempo brevissimo (un esempio potrebbe essere il flash di una macchina fotografica).
Beh, il mio amico non sapeva tutto quello che sapevo io sul condensatore, anzi, probabilmente non aveva neanche la benché minima idea su come funzionasse, eppure sapeva come usarlo, sapeva dove inserirlo in un circuito e cosa avrebbe provocato: sapeva che cos'era realmente un condensatore.
Una volta tornato a casa, cercai sul libro di fisica e trovai, insieme ad un sacco di altre formule, qualche riga sulla sua utilizzazione concreta:"...vengono usati per ridurre le fluttuazioni della tensione degli alimentatori, per generare o rivelare onde elettromagnetiche a radiofrequenza e quindi anche nella radio e nella televisione.
I condensatori, inoltre, trovano impiego come dispositivi per studiare il moto delle cariche nel campo elettrico generato fra le armature; la deviazione del puntino luminoso sullo schermo di un oscillografo è dovuta all'azione del campo elettrico di un condensatore su un fascio di elettroni che lo attraversano".In dieci pagine che in cui si spiegava il funzionamento di questo strumento, vi erano solamente una decina di righe che toccavano l'aspetto pratico della spiegazione; allora a che pro imparare a memoria formule su formule se poi non si conosce l'aspetto più semplice e immediato di quello che si è studiato: la praticità?
Il programma della V liceo scientifico è incentrato sull'elettromagnetismo, ma quando uno studente esce dal liceo, non sa nemmeno dove mettere le mani in un circuito d'appartamento o in un qualsiasi circuito di televisione o di radio. In molti si giustificano dicendo che il liceo scientifico non è un istituto tecnico, ma a che cosa serve tutto ciò che si impara in teoria se poi non si ha la benché minima idea di cosa questo significhi in pratica?
Io trovo che se tutte le ore di fisica fatte in cinque anni (pensate che sono più di trecento!) fossero svolte tenendo conto dell'aspetto pratico della materia, non dico che dal liceo uscirebbero dei tecnici, ma almeno delle persone ingegnose e pronte a risolvere ogni piccolo problema quotidiano relativo agli argomenti studiati, e questo è molto di più che persone che ricordano a malapena qualche regola e qualche formula.
Mi rendo conto che sto implicitamente estremizzando la mia posizione in questi discorsi; faccio ammenda e preciso: perchè non dev'essere possibile accompagnare costantemente alle nozioni teoriche delle nozioni "operative" e delle "pratiche" che, oltre a dare un senso concreto a ciò che si studia, rendano lo stesso studio più attraente e vivo? Oppure: non è possibile procedere induttivamente dall'esperienza alle formule, alle definizioni?
In alcuni casi, è vero, ciò non è possibile; ma sono certo più numerosi quelli in cui si può essere più "induttivi", più "naturali", meno "artificiali".
2. MATEMATICA"Qualche tempo fa mi capitò di incontrare a Copenhagen una ragazza quattordicenne che aveva passato tre anni a Summerhill dove aveva imparato a parlare l'inglese alla perfezione. 'Immagino che in Inglese sarai la prima della classe', le dissi.
Mi rispose con una smorfia afflitta: 'No, sono l'ultima della classe perché non so la grammatica'. Credo che questo sia il migliore esempio di quel che gli adulti pensano debba essere l'educazione."
(Alexander S. Neill)Quando un ragazzo esce da un qualsiasi tipo di scuola, è un dato di fatto che abbia affrontato un discreto numero di materie e che possa esibire una certa conoscenza in ognuna di queste. Ma avete mai provato a chiedere ad uno di questi di parlarvi di Pascoli, o di Verga, o di Newton o del teorema di Cauchy? La risposta che otterreste è, nella migliore delle ipotesi, una sfilza di nozioni ordinate in un discorso dal quale non potrete tirar fuori nulla di più che da un manuale di storia, di filosofia, di italiano, di fisica... Nozioni, nozioni, nozioni e ancora nozioni!
Eppure tutti sanno che c'è una bella differenza tra il memorizzare una materia e il conoscerla; c'è una persona che considero brillante in matematica, ad esempio, e che più volte mi è stata d'aiuto, ma non è mai stata valorizzata adeguatamente a scuola.
Il punto è che l'imparare un qualcosa non comporta sempre il capirlo, anzi... ed è proprio qui che entra in gioco la bravura dell'insegnante: uno studente può aver dei bei voti in filosofia eppure non capirci niente, così come può parlare benissimo in inglese ed avere insufficiente. A che cosa serve saper parlare di Kant quando non si ha la benchè minima idea di cosa in realtà significhi quello che si sta dicendo, e a che cosa serve a chi sa parlare l'inglese di imparare qualche stupida regola che sa applicare ma non citare?
Non è detto che chi esce dal liceo con un buon voto di maturità possa essere competente nelle materie studiate, e per competente intendo il conoscere una disciplina tanto da poterne discutere e da poterla utilizzare nella vita di tutti i giorni; non di rado sono le persone che hanno studiato di meno ma pensato di più che riescono a rendere utile il tempo passato sui libri e ad utilizzare in modo appropriato le conoscenze acquisite.
La scuola valorizza una parte dell'apprendimento che, benchè risulti utile, non è assolutamente la più importante.
Vorrei provare a farvi un esempio; enuncerò e dimostrerò un qualsiasi teorema matematico così come mi viene insegnato a scuola:Teorema di Rolle
Se una funzione è continua in un intervallo chiuso e limitato [a,b], è derivabile in ]a,b[ e assume valori uguali agli estremi:
f(a)=f(b) esiste almeno un punto x0 interno all'intervallo in cui la sua derivata si annulla:
f'(xo)=0 Dimostrazione
Essendo la funzione continua nell'intervallo chiuso e limitato [a,b], per il teorema di Weierstrass ammette, nell'intervallo, dei punti di massimo e minimo locali. Prendiamo in considerazione due eventualità:1 Se il minimo m e il massimo M vengono assunti in due soli punti che coincidono con gli estremi, essendo per ipotesi f(a)=f(b), ne segue che m=M; se il minimo coincide con il massimo, detto c il loro valore, ne risulta che:
c<=f(x)<=c e cioè:
f(x)=c Allora la funzione risulta una costante, quindi la sua derivata è sempre nulla.
2 Se il minimo o il massimo o entrambi vengono assunti in punti interni all'intervallo, si prenda per esempio x0 tale che f(x0)=M. Poichè x0 è un punto di massimo interno ad [a,b] e la funzione è derivabile in tutti i punti di ]a,b[, e quindi anche in x0, per il teorema secondo il quale nei punti di massimo o minimo locali di una funzione derivabile interni al dominio la derivata vale 0, si avrà:
f'(xo)=0 Definizioni e dimostrazioni di teoremi come questa vengono perlopiù imparate a memoria, e questo risulterebbe assolutamente inutile se lo scopo dell'insegnamento della matematica fosse compiere una vera analisi del teorema, capirlo e provare ad elaborare una propria dimostrazione. Io ho fatto un tentativo di rielaborare sia la definizione che la dimostrazione, ho provato ad analizzarle e a riscriverle in termini comprensibili anche per chi non conosce la matematica; questo è quello che ne è venuto fuori:
In parole povere il teorema dice che, presi due punti a e b posti alla stessa altezza, quindi con le stesse coordinate y, e disegnata una qualsiasi curva che parta da a e arrivi a b, questa abbia almeno in un punto la tangente orizzontale, quindi parallela all'asse delle x.

Ammesso per ipotesi che la curva non possieda angoli, è ovvio stabilire che il punto, o meglio, i punti in cui la tangente alla curva è orizzontale siano quelli nei quali la curva da crescente (in "salita") diventa decrescente (in "discesa"), e viceversa. Ma dato che in matematica la parola "ovvio" è poco usata, cerchiamo di dimostrare anche quest'ultima parte: suddividendo in piccolissime parti la curva, scopriamo che in realtà questa è formata da una moltitudine di brevissimi segmenti che formano tra di loro un angolo molto vicino ai 180°. Notiamo che nei punti in cui la curva passa dall'essere crescente all'essere decrescente, e viceversa, i segmenti si "raddrizzano" sempre di più fino a diventare orizzontali, per poi "ricurvarsi" e tornare a scendere o a salire; sapendo che la tangente di una retta è la retta stessa, ne deduciamo che in questi punti la tangente è orizzontale.
Ora distinguiamo i due casi:
1 Se a e b sono uniti da una retta, qualsiasi punto preso su di questa avrebbe tangente orizzontale, essendo per ipotesi questa retta orizzontale ("la tangente di una retta è la retta stessa").
2 Se invece tra a e b passa una curva qualsiasi, dovranno per forza esserci uno o più punti interni all'intervallo nei quali la curva da crescente diventa decrescente o viceversa, poiché altrimenti non potrebbe assolutamente ritornare all'altezza di partenza.Sicuramente qualsiasi professore di matematica inorridirebbe nel sentire una dimostrazione del genere, piena di termini impropri e di imprecisioni, ma al contrario molti studenti, magari non particolarmente portati per la matematica, afferrerebbero il vero significato del teorema e riuscirebbero a capirlo meglio: potrà sembrare strano, ma ho fatto leggere la "mia dimostrazione" a qualche coetaneo, che mi ha confessato di non aver mai capito il teorema ma di averlo semplicemente imparato a memoria, dimostrazione compresa.
Trovo sia fondamentale che gli argomenti trattati vengano capiti, e per permettere ciò è necessario che i metodi di insegnamento siano più comprensibili da parte di tutte le tipologie di alunno: non è assolutamente detto che un allievo con una mente poco matematica che frequenta il liceo scientifico, debba poi studiare matematica e fisica per tutta la vita, mentre è sicuro che chi è portato per le materie scientifiche, le imparerà, qualsiasi sia il modo in cui gli vengono insegnate, e in ogni caso chi capisce ricorda a lungo, mentre chi impara a memoria spesso dimentica in fretta.
3. ITALIANO-STORIA DELL'ARTE"...se per qualche motivo un insegnante non può tenere la sua lezione nel giorno stabilito, agli allievi generalmente la cosa dispiace molto. [...]
Pochi anni fa, all'Assemblea Generale, qualcuno propose di punire un colpevole con la sospensione delle lezioni per una settimana. Gli altri allievi protestarono ritenendo la punizione eccessiva."
(Alexander S.Neill)Appena il bidello entra in classe, già si vede qualche occhio che si illumina; l'insegnante prende il foglio e inizia a leggere: "Domani entrerete un'ora dopo, la professoressa di matematica è assente".
A questo punto, la felicità è così grande che invade tutta la classe: c'è un momento di caos, tutti si alzano in piedi, stringono le mani ai compagni di banco, si abbracciano...Dopo qualche minuto torna la calma, ma negli occhi di ogni studente si può intravedere la mattinata del giorno dopo, con un'ora in meno di matematica e un'ora in più di sonno.
In questo modo ho messo due immagini a confronto: degli studenti rattristati per un'ora di insegnamento persa e degli studenti gioiosi per lo stesso e identico motivo; come si può spiegare tutto ciò?
Ci ho pensato a lungo, e questo è quello che ne è venuto fuori: lo studente di oggi non è più spinto da un interesse per le lezioni, da un interesse nell'imparare cose nuove, dalla voglia di conoscere. Purtroppo, il costringere uno studente ad imparare qualcosa è assolutamente controproducente, nel senso che oramai si è perso ogni interesse vivo per la cultura: uno studente che al liceo passa notti insonni a studiare Hegel, raramente lo fa perchè effettivamente Hegel e la filosofia gli piacciono; lo fa tuttalpiù per prendere un buon voto nell'interrogazione e, dopo questa, gli interessa poco che le conoscenze assimilate rimangano nella sua testa.
Oramai la scuola è diventata un obbligo faticoso al quale si deve in ogni caso adempiere, quindi anche le materie studiate, a furia di essere imposte, diventano noiose.
Molte volte mi capita di pensare al tempo in cui Platone insegnava nell'Accademia, agli studenti che facevano a gara per poter ricevere il suo insegnamento, che affrontavano lunghi viaggi pur di sentir parlare il filosofo: e lui che cosa insegnava? Insegnava tutto ciò che un uomo poteva sapere a quel tempo.
Deve far riflettere il fatto che adesso tutto lo scibile umano (ed è molto di più di quello che si poteva sapere 2300 anni fa) è racchiuso in milioni di libri, che a scuola ne viene insegnata una parte, ma che gli studenti fanno a gara per fuggire dalla scuola, piuttosto che per entrarci.
Il fatto è che si è perso tutto il piacere che c'è nell'imparare, quindi non si studia più per una soddisfazione personale, ma per un bel voto, e purtroppo di questo ci s'accorge troppo tardi. Conosco più di una persona che è uscita dal liceo con voti alti e ora fa l'università, ma che soltanto dopo qualche anno si è accorta di non conoscere adeguatamente la storia, e solo adesso si è messa a studiare un manuale con vero interesse: pensate a quanto tempo ha buttato via studiando per un voto!
Un'amica mi spedì, il mese scorso, una cartolina da Madrid. Rappresentava un quadro intitolato "Un Mundo" (Angeles Santos), e sul retro, di sua mano, l'amica aveva riportato per intero e con precisione l'"Infinito" di Leopardi.
[...]Sempre caro mi fu quest'ermo colle,
e questa siepe, che da tanta parte
dell'ultimo orizzonte il guardo esclude.
Ma sedendo e mirando, interminati
spazi al di là da quella, e sovrumani
silenzi, e profondissima quiete
io nel pensier mi fingo; ove per poco
il cor non si spaura. E come il vento
odo stormir tra queste piante, io quello
infinito silenzio a questa voce
vo comparando: e mi sovvien l'eterno,
e le morte stagioni, e la presente
e viva, e il suon di lei. Così tra questa
immensità s'annega il pensier mio:
e il naufragar m'è dolce in questo mare.G. Leopardi
A scuola avevo imparato una serie di "nozioni" su questa poesia:È stata scritta da Giacomo Leopardi, nato nel 1798 a Recanati; la sua infanzia, dominata dal padre, intellettuale reazionario, e dalla madre energica e bigotta, si conclude con sette anni di studio "matto e disperatissimo", dai quali esce fisicamente rovinato, ma eccezionalmente colto. In questa età compone testi letterari che imitano i modelli classicistici dominanti (tragedie, liriche, epigrammi) e opere erudite. Nel 1817, dopo aver conosciuto Pietro Giordano, classicista che gli offrirà sempre stima e conforto, inizia la stesura dello Zibaldone, un diario in cui annota fino al 1831 osservazioni su temi personali, filosofici e letterari. Nel 1819, dopo il manifestarsi dei sintomi di una grave malattia agli occhi, tenta di nascosto la fuga da Recanati, ma viene scoperto e la sua prigionia a casa riprende; è anche l'anno che segna la svolta ideologica dalla fede ad una visione materialistica della realtà, da una letteratura stilisticamente elaborata e moralmente nobile alla concezione di una poesia-filosofia. Negli anni successivi compone le canzoni filosofiche e gli idilli (tra cui L'infinito). È questa la fase del cosiddetto "pessimismo storico", secondo cui gli uomini dell'antichità erano felici in quanto ingannati dalle illusioni offerte dalla Natura, mentre i moderni sono infelici perchè la ragione ha loro svelato la verità di un'esistenza dominata dalla precarietà e dal dolore.
Primo tra gli idilli, L'infinito ha uno spicco eccezionale nella poesia leopardiana; in esso Leopardi comincia a dar forma alla sua concezione di una liricità incentrata sulla ricerca di un linguaggio tendente al "vago" e all'"indefinito" e sull'esplorazione della soggettività (poeta che parla in prima persona, memorie personali, ambientazione in luoghi familiari).
Il breve componimento si può così scomporre:vv.1-3 indicazione, ma senza limiti descrittivi, di uno spazio concreto (l'area ristretta delimitata dalla siepe) e di uno specifico personale (la consuetudine del salire sul colle e lo stato d'animo che vi si accompagna);
vv.4-8 processo di astrazione, visione mentale dello spazio. Il passaggio dal primo momento a questo successivo è accentuato dall'avversativa con cui si apre il periodo (v.4 Ma) e dai due gerundi ("sedendo e mirando") che indicano non un'azione definita ma una durata;
vv.8-13 un evento minimo (v.9 "odo stormir") segna il trapasso dall'immaginazione spaziale a quella temporale. Si instaura la contrapposizione tra spazio concreto e tempo presente (voce del vento "tra queste piante" e suono della stagione "presente e viva") / spazio e tempo immaginati nel pensiero (silenzio dello spazio e delle "morte stagioni");
vv.13-15 il pensiero smarrisce; lo smarrimento genera piacere.È possibile inserire Leopardi nella tendenza generale della cultura ottocentesca a rappresentare la lingua spaziale, e cioè il concetto di spazio che consente poi di situare esperienze e oggetti; descrive quindi quella che considera la base del testo, il modello spaziale su cui esso è costruito (opposizione tra uno spazio interno e uno spazio esterno separati da una differenza di cui la siepe è il segno visibile). Si possono individuare le tensioni e le contraddizioni che generano movimenti contrapposti nelle due parti in cui il testo si può dividere: nella prima è l'esterno che penetra nell'interno grazie all'operazione della coscienza che lo assorbe e lo domina, nella seconda è il mondo interno che si disperde e si dissolve nell'esterno (Lotman).
Avrei imparato in seguito che il quadro è stato dipinto da Angeles Santos, nato nel 1912 e non ancora morto; che è un esponente del surrealismo spagnolo; che questo movimento, rifacendosi alla tradizione romantico-simbolista, vuole abolire ogni frontiera, arricchendo il "conscio" con l'"inconscio". Avrei imparato che la particolarità del dipinto sta nella centralità del mondo, che si trova tra la luce del sole e il buio della notte, che è abitato da angeli buoni che si elevano verso il cielo, e angeli cattivi che accendono delle fiaccole dal sole.
Ma a scuola non avevo mai capito quanto fosse bella questa poesia, quanto Leopardi fosse riuscito a trasmettere un sentimento così profondo e complesso in solo 15 versi, quanto fossero forti le parole usate e quanta tristezza si poteva intravedere tra queste. Non avevo mai apprezzato la sua musicalità, soprattutto se letta guardando il "dipinto" di Santos; non avevo mai provato il piacere di perdermi tra le righe e tra i colori, provando ad interpretare con i miei sentimenti ciò che entrambi gli artisti volevano comunicare.
Avevo scoperto quanto in realtà amavo la poesia e la pittura, e non me lo sarei mai immaginato!
Scopersi solo dopo quanto pittura e poesia, unite alla musica (non ho mai capito perchè questa non si studia a scuola), si completassero a vicenda formando un tutt'uno fantastico e inscindibile.
So che, come un professore di ed. fisica non può insegnare l'agilità, così un professore di letteratura o di arte non può insegnare il gusto o l'espressione, ma mentre l'insegnante di ginnastica propone degli esercizi per poter raggiungere lo scopo prefissato, l'insegnante di italiano non fa altro che interpretare, a modo suo o secondo i canoni di importanti studiosi, le poesie che si trova davanti; non mi è mai capitato, in cinque anni di liceo, di sentirmi chiedere: "Allora, dimmi cosa ne pensi di questa poesia, dimmi che sentimenti ti trasmette, dimmi che interpretazione ti piacerebbe dare a questo passo...".
A scuola non si può insegnare a diventare artisti o poeti, ma si può indicare la giusta strada per apprezzare la poesia e l'arte: un ragazzo che esce dal liceo, se ha studiato, è in grado di fare un commento e una parafrasi quasi perfetti di una qualsiasi tra le poesie affrontate durante l'anno, ma sono pochi i ragazzi che riescono ad apprezzare davvero la poesia, e se ne sono in grado non è assolutamente detto che l'abbiano imparato a scuola.
Trovo che questo sia uno dei tanti esempi di come la scuola renda noioso ciò che in realtà è bellissimo e piacevole, impoverendo lo studente di un aspetto unico e importantissimo: il sentimento..
- continua -